L’entropia, in fisica, è una grandezza scalare che rende conto della propensione di un corpo o di un sistema fisico, durante processi chimici e termodinamici, a scambiare o trasformare energia in un certo modo piuttosto che in altri. Nella fattispecie, si può dire che un sistema fisico tende a modificarsi o interagire con altri sistemi in modo da aumentare la propria entropia, o quantomeno a non farla diminuire.
La prima definizione di entropia è legata allo sviluppo della termodinamica. La parola “entropia” fu introdotta per la prima volta nel mondo scientifico da Rudolph Clausius nel 1864 e ricalcava la parola “energia”: se questa, dal greco antico, significa “capacità di agire (ergon) interna (en)”, entropia significa la capacità intrinseca di un sistema (en) di trasformarsi (tropé vuol dire “stravolgimento, declinazione”, dunque anche “trasformazione”).
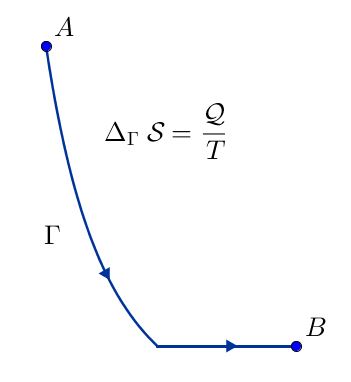
Per definire questa grandezza fisica, occorre considerare un sistema termodinamico che compia una trasformazione: supponiamo che in principio il sistema si trovi in uno stato termodinamico $A$ ed arrivi, mediante una trasformazione che chiamiamo $\Gamma$, in uno stato $B$. Ricordiamo che gli stati termodinamici sono determinabili mediante i valori (dette appunto coordinate termodinamiche) del volume $V$ occupato dal sistema, della pressione $P$ cui è sottoposto e della temperatura $T$ in cui si trova; mentre le trasformazioni termodinamiche sono cambiamenti di queste quantità, che comportano il passaggio da stadi intermedi, e coinvolgono scambi di energia tra il sistema in questione ed altri sistemi fisici, o l’ambiente, mediante lavoro e calore.
Supponiamo allora che nella nostra trasformazione $\Gamma$ si scambi una certa quantità di calore $\mathcal{Q}$, ad una temperatura (assoluta) $T$. Definiamo quindi la variazione di entropia $\Delta \mathcal{S}$, lungo la trasfomazione $\Gamma$, come il rapporto tra il calore scambiato e la temperatura alla quale viene scambiato: $$ \Delta_{\Gamma} \mathcal{S} \ = \ \frac{\mathcal{Q}}{T}$$
Per sua stessa definizione, l’unità di misura dell’entropia, nel sistema internazionale, è pari all’unità di misura dell’energia, il Joule $\text{J}$ in cui si misurano gli scambi energetici (tra cui il calore), fratto l’unita di misura della temperatura assoluta, il gardo kelvin $\text{K}$.
Notare che non abbiamo definito l’entropia, ma solo variazioni della stessa. Queste variazioni sembrano essere inoltre legate alla trasformazione che porta un sistema termodinamico da uno stato all’altro: insomma, una definizione assai poco precisa.
Ma ecco che i principi della termodinamica ci vengono in aiuto: tramite il secondo principio della termodinamica, l’entropia diviene indipendente dalla trasformazione seguita, e può essere determinata grazie al terzo principio, che stabilisce uno zero per la scala dell’entropia. Ma procediamo con ordine.
Ricordiamo l’enunciato di Clausius del secondo principio della termodinamica:
- "non è possibile costruire una macchina termica il cui unico risultato sia il trasferimento di calore da una fonte di calore a temperatura inferiore a una fonte di calore a temperatura superiore."
Quindi, “naturalmente”, cioè senza l’apporto di lavoro esterno o di altre forze, gli scambi di calore avvengono solo in un verso: da un corpo più caldo ad un corpo più freddo. Per la convenzione sui segni del calore, un calore positivo $\mathcal{Q} > 0$ corrisponde ad un sistema che assorbe calore; essendo la variazione di entropia, lungo una particolare trasformazione, definita come $\Delta_{\Gamma} \mathcal{S} = \frac{\mathcal{Q}}{T}$, ad un calore positivo corrisponde una variazione di entropia positiva, ossia un aumento di entropia (la temperatura, essendo assoluta, può assumere solo valori non negativi, e quindi non influisce sul segno della variazione di entropia). Possiamo quindi concludere che un sistema che riceva calore aumenta la propria entropia, e che questa situazione si presenta qualora non intervengano fattori esterni.
Ma il secondo principio della termodinamica ha altre implicazioni, più profonde a livello matematico, sull’entropia. Occorre prima introdurre però il concetto di funzione di stato.
In generale, in fisica, esistono grandezze che dipendono da altre. Se abbiamo delle grandezze primitive, “indipendenti” (spesso scelte come coordinate di un certo sistema di riferimento), ad una variazione di queste seguirà anche una variazione di quelle dipendenti. Nella cinematica classica, detta newtoniana, se pensiamo alle coordinate spaziali e al tempo come grandezze indipendenti, possiamo determinare la variazione di posizione, velocità, potenza, lavoro, impulso, eccetera, in base alle relazioni matematiche che legano le prime grandezze alle seconde: ad esempio, se la posizione di un corpo varia di $\Delta x$ in un tempo $\Delta t$, la velocità del corpo si può calcolare come $\frac{\Delta x}{\Delta t}$.
Alcune grandezze non dipendono dal modo in cui avviene la variazione delle variabili indipendenti: la velocità posseduta da un corpo è sempre la stessa, che il suo moto, responsabile del cambiamento della sua posizione, sia rettilineo, circolare, o disegni qualche altra strana curva (a patto, s’intende, che lo spostamento e il tempo in cui avviene siano sempre gli stessi). Ma alcune di queste quantità dipendono dal “percorso” seguito dal sistema fisico dallo stato di partenza allo stato di arrivo: ne è un classico esempio il lavoro.
In termodinamica, si segue il medesimo ragionamento: si definiscono alcune quantità che dipendono dalla trasformazione termodinamica seguita, mentre altre no. Ad esempio, il lavoro $\mathcal{L}$ o il calore $\mathcal{Q}$ scambiati in una trasformazione dipendono dalla trasformazione stessa; il primo principio della termodinamica asserisce che, invece, la differenza $\mathcal{Q} - \mathcal{L}$ non dipende dal percorso seguito.
Ogni volta che ci si trova davanti ad una quantità che non dipende dalla trasformazione che l’ha comportata è sempre possibile trovare una grandezza che esprima la quantità in esame come differenza tra due suoi valori, assunti dal sistema negli stati iniziale e finale: per riprende l’esempio del primo principio della termodinamica, la quantità $\mathcal{Q} - \mathcal{L}$, non dipendendo dalla trasformazione subita dal sistema si può scrivere come differenza fra i valore di una certa quantità, detta energia interna: $\Delta \mathcal{U} = \mathcal{U}_{\text{finale}} - \mathcal{U}_{\text{iniziale}}$. Un analogo nella meccanica classica è il potenziale: se una forza ammette potenziale $V$, ed è quindi una forza conservativa, il lavoro da essa compiuto non dipende dal percorso seguito ma è anzi pari all’opposto della differenza tra potenziale finale e potenziale iniziale: $\mathcal{L} = - \Delta V = - (V_{\text{finale}} - V_{\text{iniziale}}) = V_{\text{iniziale}} - V_{\text{finale}}$. Tutte queste quantità vengono dette funzioni di stato, siccome non dipendono dalle variazioni e dai cambiamenti degli stati che compongono la trasformazione cui il sistema è soggetto, ma solamente dagli stati occupati all’inizio e alla fine della trasformazione stessa.
La presenza di una funzione di stato è molto conveniente, poichè, non dipendendo dal metodo con cui viene modificato il sistema, le sue variazioni possono venire calcolate dai fisici facendo seguire al sistema una trasformazione qualsiasi: non importa quale.
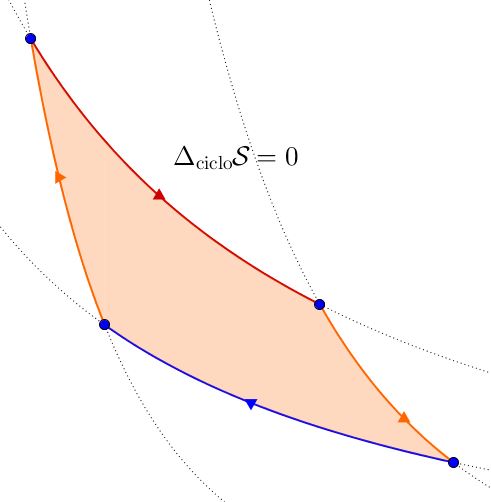
A causa della loro definizione, le funzioni di stato godono di una importantissima proprietà: lungo una trasformazione ciclica, ossia una trasformazione che riporta il sistema allo stato originale, le loro variazioni sono nulle: bisognerebbe operare, per calcolare la variazione di una variabile di stato, una differenza tra due quantità uguali, che dà sempre $0$. Questa caratteristica è talmente importante che può essere usata per identificare le funzioni di stato: se, a fronte di ogni trasformazione ciclica, si registra una variazione nulla, la quantità che si sta indagando è una funzione di stato.
Per tornare all’entropia, il secondo principio della termodinamica implica che l’entropia è una funzione di stato: le sue variazioni $\Delta \mathcal{S}$ da uno stato termodinamico ad un altro si possono calcolare mediante il rapporto $\frac{\mathcal{Q}}{T}$, ove il calore scambiato e la temperatura sono computati lungo una qualsiasi trasformazione che congiunga i due stati termodianmici di partenza e arrivo.
Questo però fa sorgere alcuni problemi. Innanzitutto, si potrebbe pensare di collegare i due stati con una trasformazione adiabatica, in cui il calore scambiato è nullo, e dunque ottenere una variazione di entropia nulla tra ogni stato termodinamico: tutti gli stati termodinamici sarebbero caratterizzati dallo stesso livello di entropia! A questa obiezione si risponde facilmente, poichè non è detto che i due stati in esame possano essere collegati da una trasformazione adiabatica.
Fugato questo primo dubbio, si potrebbe notare che la variazione di entropia, essendo essa una variabile di stato, si annulla lungo un qualunque ciclo termodinamico. Ma questo non contraddice quanto abbiamo detto in principio, cioè che l’entropia tende ad aumentare?
Innanzitutto, bisogna ricordare che il secondo principio dice che l’entropia non diminuisce: è possibile che rimanga al livello di partenza. Lungo un qualsiasi ciclo termodinamico, il fatto che l’entropia del sistema soggetto al ciclo non aumenti non costituisce un paradosso.
Quel che si può asserire, invece, è che le singole trasformazioni seguite dal sistema avverranno in direzione di entropia crescente. Questo non significache l’entropia non può diminuire: in linea di principio, fornendo una certa quantità di lavoro è possibile trasportare un sistema da livelli di entropia più alti a livelli più bassi. Ma a questo punto, il sistema cercherà di riportarsi ad un livello entropico maggiore, per compensare la perdita di entropia: mantenerlo in quello stato costerebbe (molta) energia. È questa l’essenza del secondo principio della termodinamica.
Si può comprendere questo ragionamento con un paragone. Si pensi a una pallina che si trova sul pendio di una montagna: se lasciata a se stessa, la pallina inizierà a spostarsi verso valle; ma questo non vuol dire che non sia possibile portarla a monte: occorre appunto fornire del lavoro, e tenerla in una posizione più alta ci costerebbe uno sforzo.
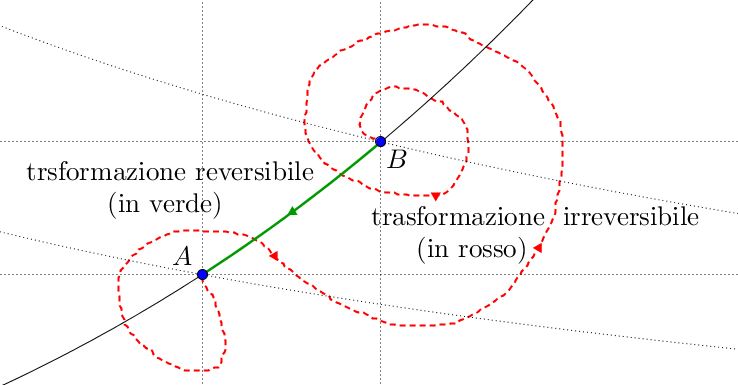
Se pensiamo che tutte le trasformazioni termodinamiche, come quelle della meccanica classica, si possano invertire, però, dobbiamo scontrarci con la dura realtà. Una trasformazione termodinamica conduce un sistema da uno stato all’altro, passando attraverso stati intermedi. Uno stato termodinamico è determinato dalle sue coordinate pressione $P$, volume $V$ e temperatura $T$. Ma essendo quantità che misurano macroscopicamente ciò che avviene in un intero sistema, se questo non si trova in una condizione di equilibrio (statico, termico e chimico), non possiamo determinarle, o quelle quantità che determiniamo sono valide solo per una porzione limitata del nostro sistema. È ben chiaro allora quale sia il problema: una trasformazione, per sua stessa definizione, comporta uno squilibrio tra gli elementi di un sistema: come facciamo a misurare una condizione di equilibrio se l’equilibrio non c’è? È assai probabile quindi, che in una trasformazione termodinamica gli stati intermedi non possano essere determinati: eseguire i calcoli, che la teoria prevede per trasformazioni passanti tra stati perfettamente determinati, è spesso impossibile nella pratica.
Queste trasformazioni, coinvolgendo stati di disequilibrio in cui le coordinate termodinamiche non possono essere determinate, non possono essere invertite: sarebbe come pretendere di ritornare alla partenza, senza sapere quale percorso si è seguito. Per questo motivo sono dette trasformazioni irreversibili. La parola rende conto della nostra realtà: sarebbe ben strano un mondo in cui, bruciando “in modo inverso” il carbone si possa ottenere della legna.
Se un sistema segue una trasformazione irreversibile, portandosi da uno stato $A$ ad un altro stato $B$, magari è possibile ricondurlo dallo stato $B$ allo stato $A$ mediante una trasformazione reversibile, ottenendo un ciclo termodinamico: il sistema verrà riportato al livello di entropia originario, ma la nostra entropia, l’entropia dell’ambiente, o dell’agente, qualunque esso sia, che ha riportato il sistema allo stato $A$, aumenta.
Quando si dice, nel linguaggio comune, che “l’entropia misura il disordine dell’universo”, si intende che i sistemi fisici, la realtà in cui viviamo, tende naturalmente verso stati ad entropia maggiore, e per riportarla ad entropia minore occorre spendere energia: in generale, in quantità maggiore di quanta il sistema ne ha spesa per portarsi allo stato ad entropia maggiore, ma senza dubbio mai inferiore a quel valore. Il secondo principio della termodinamica non è quindi solo un principio astratto di una disciplina scientifica, ma rende conto di quanto accade nella realtà. Un po’ come tutti i principi della fisica.
Inoltre l’entropia, rispetto alle altre funzioni di stato, dispone di una marcia in più: sussiste infatti il terzo principio della termodinamica.
Delle funzioni di stato è agevole calcolare le differenze, ma non è dato di sapere (a dispetto del loro nome) il valore preciso di una funzione di stato in un particolare stato. Supponiamo infatti di avere una certa funzione di stato $f$, e di due stati che chiameremo, per semplicità, $1$ e $2$. Sappiamo calcolare $\Delta f$, ma per calcolare $f(1)$ o $f(2)$ come facciamo? Possiamo calcolare uno dei due valori sapendo l’altro: difatti, siccome $\Delta f = f(2) - f(1)$, allora $f(2) = f(1) + \Delta f$ o, equivalentemente, $f(1) = f(2) - \Delta f$. Ma non possiamo prescindere da uno dei due valori $f(2)$ o $f(1)$.
Quel che operativamente si fa, è di porre la funzione di stato, in uno stato arbitrario (ma comodo), pari ad un valore arbitrario (ma comodo). Ad esempio, il potenziale elettrico è definito di modo che, in punto infinitamente lontano, sia nullo. Ma tutte queste considerazioni sono una scelta fatta da chi opera i calcoli: io potrei benissimo stabilire che il potenziale elettrostatico sulla cima del monte Everest vale $7 \ text{ V}$ (Volt); le differenze di potenziale, comunque, resterebbero le stesse anche dopo questo bizzarra decisione.
Ma l’entropia, sebbene sia una funzione di stato, non ha bisogno di decisioni arbitrarie per stabilire un valore di partenza: il terzo principio della termodinamica, o meglio, il teorema di Nernst, implica che l’entropia vale $0$ alla temperatura assoluta di $0$ gradi.